This paper studies the effect of self-interaction errors on the barrier heights of chemical reactions. For this purpose we use the well-known Perdew-Zunger self-interaction-correction (PZSIC), as well two variations of the recently developed, locally scaled self-interaction correction (LSIC) to study the barrier heights of the BH76 benchmark dataset. Results show that both PZSIC and especially the LSIC methods improve the barrier heights relative to the local density approximation (LDA). The version of LSIC that uses the iso-orbital indicator z as a scaling factor gives a more consistent improvement than an alternative version that uses an orbital-dependent factor based on the ratio of orbital densities to the total electron density. It is shown that LDA energies evaluated using the self-consistent and self-interaction-free PZSIC densities can be used to assess density-driven errors. The LDA reaction barrier errors for the BH76 set are found to contain significant density-driven errors for all types of reactions contained in the set, but the corrections due to adding SIC to the functional are much larger than those stemming from the density for the hydrogen transfer reactions and of roughly equal size for the non-hydrogen transfer reactions.
Introduction
Density functional theory (DFT) calculations with approximate semi-local exchange-correlation functionals fail to predict certain properties such as band gaps, reaction barriers, and fragment dissociation energies due to the self-interaction error (SIE). It is known that SIE arises from the in-complete cancellation of the self-Coulomb interaction by the density functional approximation (DFA) of the self-exchange energy for a one-electron density. The effect of SIE is particularly noted for systems with stretched bonds such as transition states in chemical reactions. With DFAs, the total energy of an N-electron system deviates from piece-wise linearity between integer numbers of electrons. The total energy of an N-electron system varies as a convex curve as a function of charge between N and N + 1 electrons which is known as the charge delocalization problem.
The self-interaction correction method of Perdew and Zunger (PZSIC) employs an orbital-by-orbital correction scheme to remove the one electron SIE. Al-though PZSIC performs well in describing properties that are strongly impacted by SIE, it tends to over-correct equilibrium properties that are already described well by semi-local DFAs. This is known as the “paradox of SIC.” Non-empirical local or semi-local density functionals such as the Perdew-Wang local density approximation (LDA) or the Perdew, Burke, and Ernzerhof (PBE) generalized gradient approximation (GGA) are designed to be exact in the limit of uniform electron density, and it has been argued that satisfying this constraint is important for achieving accurate descriptions of molecules. But when PZSIC is applied, the corrected DFAs violate this constraint.
In this approach, called the locally scaled SIC (LSIC) method, an iso-orbital indicator is used to determine the nature of the charge density at a given point in space, distinguishing one-electron-like regions from regions where the density is slowly-varying and many-electron-like. The self-exchange and self-Coulomb energy densities of each orbitalare then scaled locally such that full SIC is maintained in one-electron regions, but scaled down in slowly-varying regions.
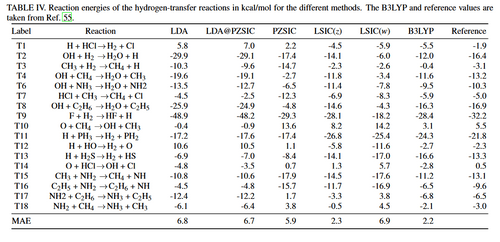
In this work, the performance of PZSIC and LSIC for chemical reaction barriers is examined. The methods have been tested previously on the small set of reactions known as BH6 where it was found that both PZSIC and LSIC improve the calculated reaction barriers over uncorrected DFAs. Here the tests are extended to the larger BH76 bench-mark set. The BH76 set has been used previously to benchmark other methods and has been updated over the years and incorporated into more comprehensive benchmark sets. Results are reported using PZSIC and two LSIC methods that use different schemes for scaling the SIC.
All calculations were performed using the FLOSIC code. The calculations were done at the all-electron level, using an extensive Gaussian basis set optimized for the PBE functional. For first row atoms, a typical basis includes 5 s, 4 p, and 3 (Cartesian-type) d functions, based on between 12 and 15 single Gaussian orbitals (SGOs). For a second row atom, atypical basis is based on 16 to 18 SGOs.
The LDA was used as parameterized in the PW92 functional for all the calculations. LSIC-LDA total energies were computed using the self-consistent FLOSIC-LDA density and optimized FODs.
Conclusion
The performance of SIC was examined on reaction barrier heights and the energies of the HT and NHT reactions in the BH76 benchmark set, using both the traditional Perdew-Zunger SIC (PZSIC) and locally scaled variations (LSIC(z)and LSIC(w)). The reaction barriers were strongly underestimated by LDA. The LDA errors in the barriers are significantly reduced by PZSIC and reduced further by the LSIC methods, especially for the HT reactions, where the MAE forLSIC(z) is reduced to 2.8 kcal/mol (1.6 kcal/mol if one out-lier reaction is removed from the averaging).
The LSIC total energy values lie between LDA and LDA-PZSIC values because the amount of energy corrections with LSIC are different for the reactant/product states and for the transition states, LSIC barriers calculated from energy differences, do not necessarily result in values in between LDA and PZSIC. For the BH6 set of reactions, it is observed that LSIC removed overcorrection of PZSIC more on the transition states than the reactant and product states such that the barrier heights become higher than the underestimated barriers of PZSIC.
The self-interaction free density from a self-consistent PZSIC calculation can be used to probe for density-driven errors. Results from LDA@PZSIC calculations are qualitatively similar to those of LDA@HF, with both approaches predicting that reaction barriers are subject to significant density-driven errors, but that the corresponding reaction energies are not. The full correction due to the use of the SIC energy functionals is, however, much larger for the overall BH76 set than the corrections from either LDA@HF or LDA@PZSIC calculations and shows significant corrections arising from the functional correction. The LDA@PZSIC results suggest smaller density-driven errors than LDA@HF on average.
The LSIC method describes reaction barriers well when applied in conjunction with the LDA, but the LDA is the simplest DFA and is relatively inaccurate for molecular properties. It remains a challenge to develop an LSIC-like method for more accurate generalized gradient approximations (GGAs) and meta-GGAs.




