Publication: Journal of Chemical Physics

This paper examines the role of self-interaction error (SIE) removal on the evaluation of magnetic exchange coupling constants. In particular, it analyzes the effect of scaling down the self-interaction correction (SIC) for three nonempirical density functional approximations (DFAs) namely, the local spin density approximation, the Perdew–Burke–Ernzerhof generalized gradient approximation, and the recent SCAN family of meta-GGA functionals.

The characterization of the magnetic properties of materials is crucial for applications such as memory storage devices, spintronics, quantum computing, and magnetic sensors. In many cases, the magnetic behavior arises from interactions between localized electrons typically described using spin Hamiltonians, including spin–spin exchange and dipolar interactions, and magnetic anisotropy contributions. The accurate theoretical description of magnetic properties by means of electronic structure calculations is especially challenging since the energy spacing involved can be much smaller than the typical electronic excitation energies.

In recent years, the development of the Fermi-Löwdin orbital self-interaction correction (FLOSIC) methodology and software improved the accessibility of SI-free calculations. FLOSIC has been applied to study various molecular properties and showed improvement over LSDA and GGA for most cases where SIE dominates the errors.

This paper explores the potential of locally scaled SIC methods for the prediction of magnetic exchange coupling constants J. It also analyzes a more comprehensive study of coupling constants by applying three different SIC methods to the three levels of exchange-correlation approximations that include the most recent r²SCAN meta-GGA functional. Results of various SIC methods for the three different classes of systems are compared and analyzed.

All calculations were performed with the development version of the FLOSIC code.

Considering the following representative exchange-correlation functionals: the local spin density approximation (LSDA) parametrized by Perdew and Wangthe Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation (GGA) functional, SCAN, and the recent r²SCAN meta-GGA functionals. Since the SCAN functional is numerically problematic, a very dense integration mesh (roughly 45000 grid points per atom for organic molecules) specifically tailored for this functional to obtain accurate energies.  Likewise, a mesh with an intermediate grid density between GGA and SCAN for r²SCAN calculations since meta-GGAs generally require finer meshes than GGAs.

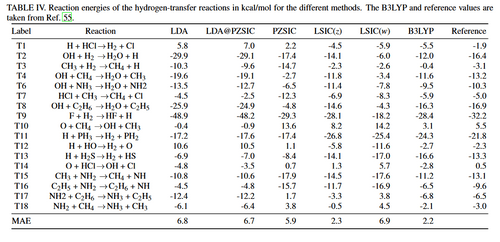
First, FLOSIC and locally scaled SIC methods for magnetic exchange coupling constants using H-He model systems are assessed. For all the H-He models, reference values from accurate wave function calculations are available. The 1s hydrogen orbitals are coupled through a super exchange mechanism mediated by the He orbitals. These simple super exchange model systems were used multiple times in the literature to assess the performance of electronic structure methods for magnetic J couplings. The smallest linear H–He–H was also used to address the effect of SIE on exchange coupling constants.Additionally, six organic biradical molecules, [C₃H₃]⁻, C₄H₄, trimethylenemethane (TMM), p-C₈H₈, m-C₈H₈, and tetramethyleneethane (TME), and chlorocuprate [Cu₂Cl₆]^2–.

Conclusion

This paper studied the magnetic exchange coupling parameters for sets of molecules: H-He models, six organic radical molecules, and [Cu₂Cl₆]^2– using DFAs with and without the SIC scheme of PZSIC. In addition, it assessed the impact of orbital-scaled SIC methods, such as OSIC and LSIC applied to LSDA to study the performance of these SIC methods on calculating the said property. For the H-He–H system using the SP method, application of PZSIC improves the resulting exchange couplings especially for PZSIC-PBE. With LSIC-LSDA, performance is slightly worsened compared to PZSIC-LSDA.

For the H–He multinuclear systems, we find that removing SIE decreases coupling strengths. PZSIC shows good performance for the three functionals. LSIC(z)-LSDA shows slightly larger discrepancies than PZSIC-LSDA for the nearest-neighbor couplings but shows better agreement for the second nearest-neighbor couplings with the reference, resulting in a relatively small MAPD for this set. The smallest MAPD is seen in the density based OSIC(w)-LSDA with SP and PZSIC-PBE with NP. For the set of organic molecules, J_SP of uncorrected DFAs shows a fair performance, while removing SIE overestimates the values notably. However, J_NP from PZSIC-DFAs coincidentally provides good agreement with the references where PZSIC-PBE and PZSIC-LSDA show two of the smallest percentage deviations. Although, it is found that the J_NP approach with LSIC and OSIC performs rather poorly, the J_SP approach combined with LSIC(z)-LSDA provides the best estimate among all SP approaches (MAPD, 18%) in terms of percentage deviations (MAPD of the rest of the methods ranging from 35 to 161%) where the triplet-singlet energy gaps of PZSIC are reduced in all six systems.

Finally, for the chlorocuprate [Cu₂Cl₆]^2–, LSIC(z)-LSDA, SCAN, and r²SCAN produce very weak antiferromagnetic couplings for θ = 0° and ferromagnetic couplings for θ = 45° showing close agreement with experiments. The DFA@PZSIC-DFA results are, in general, better than those of uncorrected DFAs but not as good as PZSIC-DFAs. Thus it seems that using an SIC density alone is not sufficient and that an SIC energy correction is also needed for this property. Among the uncorrecetd DFAs, SCAN outperforms LSDA and PBE in all cases. Also, r²SCAN closely mimics the SCAN functional. It is a good efficient alternative to SCAN due to its numerical efficiency. In all cases, it is observed that LSIC reduces the amount of SIC from PZSIC, but this reduction does not always improve the magnetic exchange couplings. This is especially true for the systems that mainly consist of single-electron regions where PZSIC already performs well. For the more complex organic systems and [Cu₂Cl₆]^2–, an overcorrecting nature of PZSIC is more pronounced when the SP approach is considered. It is found that removing excess SIC using LSIC(z) gives an improved performance over PZSIC in these cases.

In a case-by-case performance, combinations of certain functionals and SP/NP approaches work very well for a set of systems but work rather poorly for others. This includes J_SP of PZSIC-PBE, -SCAN, and -r²SCAN on H–He–H, J_NP of PZSIC-PBE and J_SP of OSIC(w)-LSDA on H-He multicenter complexes, J_NP of PZSIC-LSDA and PZSIC-PBE on organic molecules, and SCAN and r²SCAN on chlorocuprate. Thus, some care must be exerted prior to the practical application of these methods for the evaluation of magnetic exchange couplings. On the other hand, we find that the SP approach with LSIC(z)-LSDA provides a decently good overall performance across all four sets of systems, ranging from above average to a few of the best performances. This singles out the LSIC(z) method as a promising option for applications to exchange coupling constants in a wide range of systems. The performance of the LSIC method can possibly be improved further by identifying a more suitable iso-orbital indicator.

‍