Publication in the Journal of Chemical Physics

Introduction

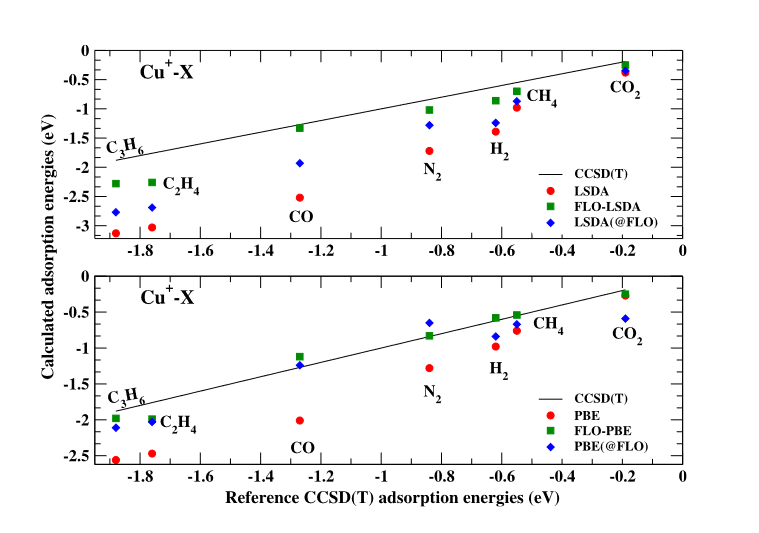
Density functional theory (DFT)-based descriptions of the adsorption of small molecules on transition metal ions are prone to self-interactionerrors. Here, we show that such errors lead to a large over-estimation of adsorption energies of small molecules on Cu+, Zn+, Zn2+, and Mn+in local spin density approximation (LSDA) and Perdew, Burke, Ernzerhof (PBE) generalized gradient approximation calculations compared to reference values computed using the coupled-cluster with single, doubles, and perturbative triple excitation method.

These errors are significantly reduced by removing self-interaction using the Perdew–Zunger self-interaction correction (PZ-SIC) in the Fermi–Löwdin Orbital (FLO) SIC framework. In the case of FLO-PBE, typical errors are reduced to less than 0.1 eV. Analysis of the results using DFT energies evaluated on self-interaction-corrected densities [DFT(@FLO)] indicates that the density-driven contributions to the FLO-DFT adsorption energy corrections are roughly the same size in DFT = LSDA and PBE, but the total corrections due to removing self-interaction are larger in LSDA.

"While self-interaction significantly impacts the calculated binding energies for the transition metal ions studied in this work (Cu+, Zn+, Zn2+, andMn+), it has almost no effect on the binding energies for Mg2+."

In our FLO-DFT calculations, we employed the PW92 LSDA functional and the PBE functional. For brevity, we refer to these calculations as FLO-LSDA and FLO-PBE. For the Cu+:X systems,we also computed adsorption energies using the SCAN functional and FLO-SCAN. The density-driven errors of an approximate functional can be reduced by evaluation of that functional not on its own self-consistent density but on a density believed to be more accurate for that purpose, such as the Hartree–Fock (HF) density.

We explored the extent to which self-interaction errors for the binding energies are density-driven by evaluating the approximate LSDA, PBE, and SCAN energy functionals using the self-consistent FLO-LSDA, FLO-PBE, and FLO-SCAN densities, respectively,which are one-electron self-interaction free. We label these calculations LSDA(@FLO), PBE(@FLO), and SCAN(@FLO). For the Cu+:X systems, we also carried out PBE(@HF) calculations of the binding energies.

For these calculations, the GAUSSIAN code41 was used with Dunning’s augmented, correlation-consistent triple-zeta basis sets (aug-cc-pVTZ). For the Cu+:X calculations, we used bond lengths taken from the Cu(I)-MFU-4l MOF model without further relaxation. For the remaining Mn+:X calculations, we optimized the atomic arrangements using the PBE functional and then used those arrangements for all methods.

Conclusion

We used the FLOSIC method to assess the impact of removing SIE from DFT for the calculation of adsorption energies for a set of closed-shell molecules on transition metal ions. We compared binding energies computed with DFT and FLO-DFT methods with results from accurate CCSD(T) calculations. Removing SIE in FLO-DFT generally corrects the binding energies in the direction of the reference CCSD(T) values, yielding much improved results compared to the corresponding uncorrected DFT results.

While self-interaction significantly impacts the calculated binding energies for the transition metal ions studied in this work (Cu+, Zn+, Zn2+, andMn+), it has almost no effect on the binding energies for Mg2+. A simple electrostatic model largely reproduces the trend in adsorbate binding energies for Cu+:X and shows that the polarization of the adsorbate in the electric field of the positive metal ion is responsible for a significant part of the binding energy. A comparison of the self-consistent total charge density from the FLO-PBE and PBE calculations for Cu+:CO shows that PBE tends to delocalize charge from near the Cu+ site to the region between Cu+ and C.

Evaluating the PBE energy using the FLO-PBE density PBE(@FLO) improves the prediction of the adsorption energy. The improvement is similar to that derived from evaluating the PBE energy using the HF density [PBE(@HF)]. The size of this density-driven contribution to the overall SIC correction is approximately the same for LSDA and PBE, but because the total correction is larger in the FLO-LSDA case, the density-driven contribution represents a larger fraction of the FLO-PBE corrections. The size of the density-driven corrections is largest for Cu+:X.